Coursework | November 2024
Poisson Image Editing
Image Processing by Prof Lourdes Agapito
University College London (UCL)
University College London (UCL)
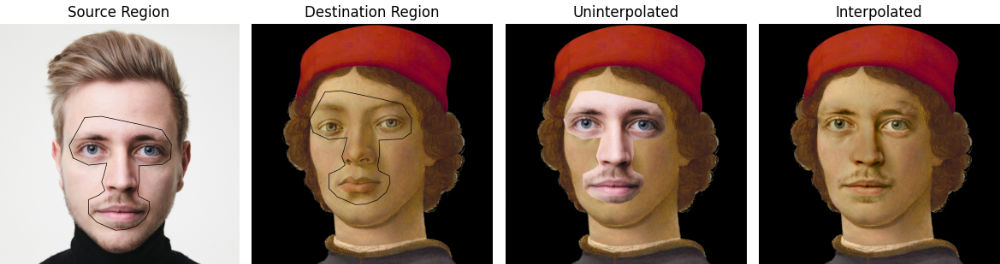
"Portrait of a Youth" [1]
During my MSc in Computer Graphics, Vision and Imaging I was lecturing a module about Image Processing in which one of my student projects focused on Poisson Image Editing. It is a seamless cloning method to transfer and interpolate a frequency pattern from an arbitrary image into another solving a poisson equation for each pixel to clone. The method was first introduced by
Perez et al. in 2003. [2]
Method
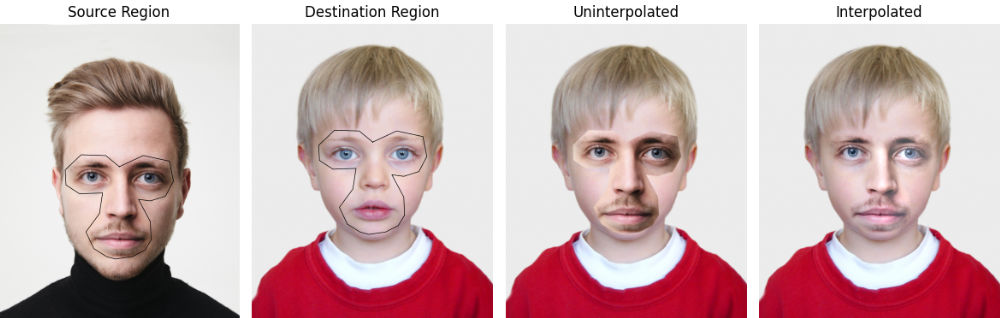
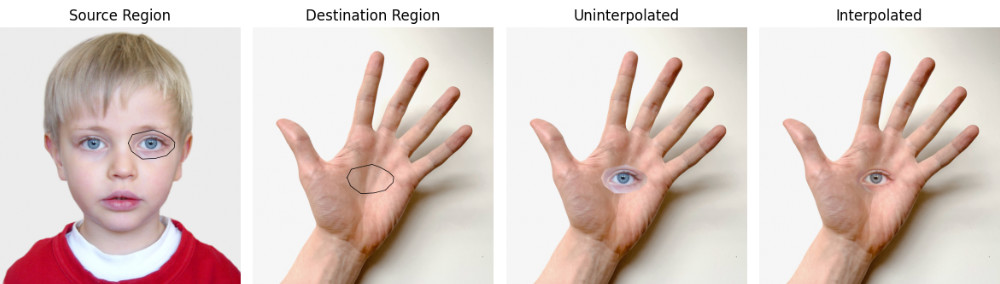
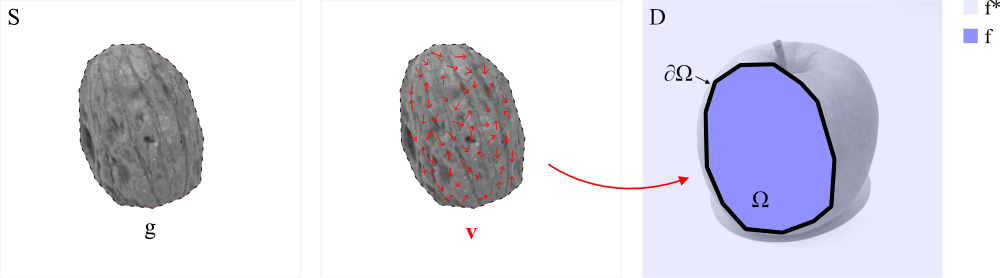
We will mainly focus on guided image interpolation, which in simple terms adjusts the image intensities over region
All we need is a destination image
All we need is a destination image
Minimizing the difference between
This gives us a linear system to solve for all
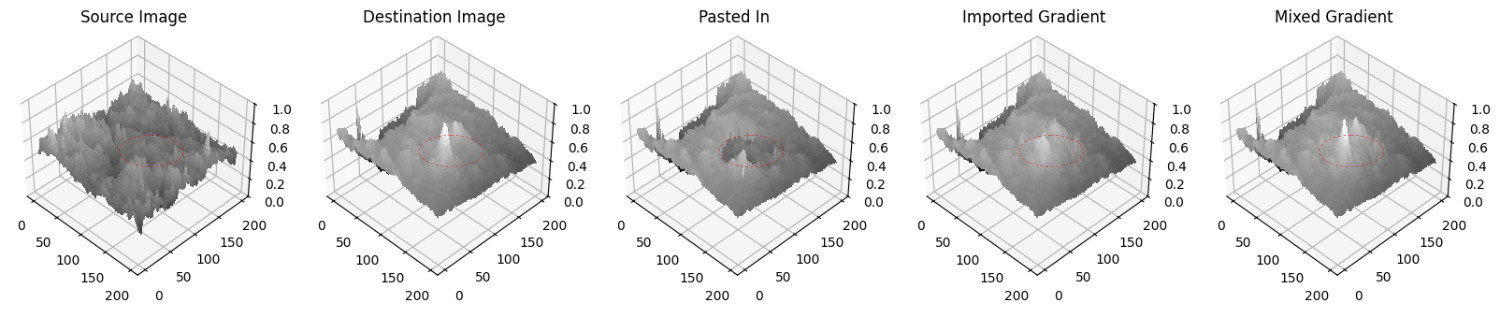
Following the method described above there are two ways to apply it for seamless cloning in images: (i) importing the gradient solely from the source image and willing to remove any details in region
In figure 3 this becomes particularly visible when comparing the specular reflections on the apple in the images but especially comparing the gradients. When importing the gradient this reflection gets blurred, when mixing it is preserved. On the other hand we showcase for reference how
In figure 3 this becomes particularly visible when comparing the specular reflections on the apple in the images but especially comparing the gradients. When importing the gradient this reflection gets blurred, when mixing it is preserved. On the other hand we showcase for reference how

So far the example was only a grayscale image. For multi-channel images one has to solve the above minimization problem for each individual channel independently. Figure 5-8 showcase this on the example of trasnfering the texture of a walnut onto an apple in RGB.
It is a widely known issue of using arbitrary images as textures for 3D models that by populating the geometry with the texture tile they create visible tiling seams which are not desired. Poisson image editing can be used to synthesise a seamless texture tile from any texture. With the above technique it is possible to take some arbitrary image and create a ‘tiling’ boundary condition
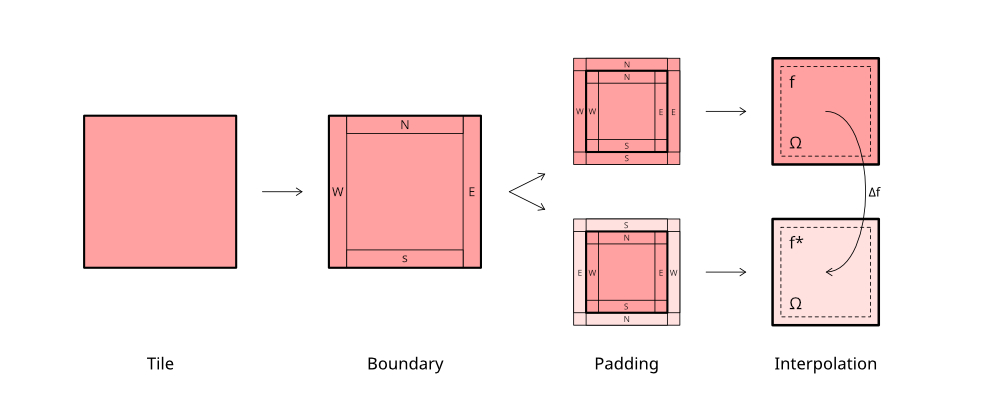
The effect of seamless tiling becomes particularly visible when applying it to a texture with big differences in illumination, given that textures mostly follow the same pattern when it comes to color and gradience. In such a case the method evenly distributes the illumination across the tile and the seam becomes nearly invisible even though the texture pattern does not match exactly. In figure 11 this illumination redistribution is made visible and indicates basically a complementary intensity to the original tile.


Results